Die Normalverteilung gehört in den Bereich der sogenannten Stochastik. Diese ist ein Teilgebiet der Mathematik. Sie umfasst zudem sowohl die Statistik als auch die Wahrscheinlichkeitsrechnung.
Das klingt kompliziert, soll dir aber nur zur Einordnung dienen, denn: Als stochastisch gelten Daten, die vom Zufall abhängen und dennoch berechnet und grafisch dargestellt werden können.
Normalverteilung «einfach erklärt»
Die «Normalverteilung» ist auch unter dem Begriff «Gaußsche Kurve» bzw. «Glockenkurve» bekannt und wird zur grafischen Darstellung von Häufigkeiten großer Datenmengen angewandt. Die Symmetrie des Graphs ist typisch für eine Normalverteilung.
Definition: Normalverteilung
Die Normalverteilung wird gelegentlich schlicht «Glockenkurve» genannt, weil ihre grafische Darstellung diese Form aufweist. Bekannter ist die Normalverteilung als «Gaußsche-Verteilung» oder «Gauß-Verteilung», da sie vom deutschen Mathematiker und Physiker Carl Friedrich Gauß (1777 – 1855) entwickelt wurde.
Angewendet wird diese Methode vor allem für die Erhebung großer Datenmengen, um die Häufigkeit bestimmter Daten oder Beobachtungen grafisch darzustellen. Dadurch können nicht nur große Datenmengen anschaulicher gestaltet, sondern gleichzeitig auch alle Abweichungen angezeigt werden. Dazu gehört beispielsweise die Erhebung der Höhen aller Gebäude innerhalb einer Stadt, das Alter der Bevölkerung in einer Stadt – oder des gesamten Landes oder auch der Bildungsstand einer Bevölkerung anhand der Schulabschlüsse und viele Daten mehr.
Die Bezeichnung «Normalverteilung» beschreibt konkret, dass es sich bei der «Glockenkurve» um ein absolut normales Ergebnis handelt. Der Funktionsgraph einer Normalverteilung ist deshalb symmetrisch und glockenförmig, kann aber sowohl gestreckt als auch gestaucht ausfallen.
Normalverteilung – die Formel zur Berechnung
Zu jeder mathematischen Kurve gehört auch eine Formel zur Berechnung des Kurvenverlaufs. Für die Glockenkurve musst du wissen, dass diese sehr steil oder auch sehr flach verlaufen kann. Es ergibt sich also nicht immer die klassische Glockenform!
Dennoch handelt es sich für gewöhnlich immer um eine Kurve mit achsensymmetrischer Verteilung der Werte. Diese zeigt dann eine symmetrische Wahrscheinlichkeitsverteilung um ihren jeweiligen Erwartungswert.1 2
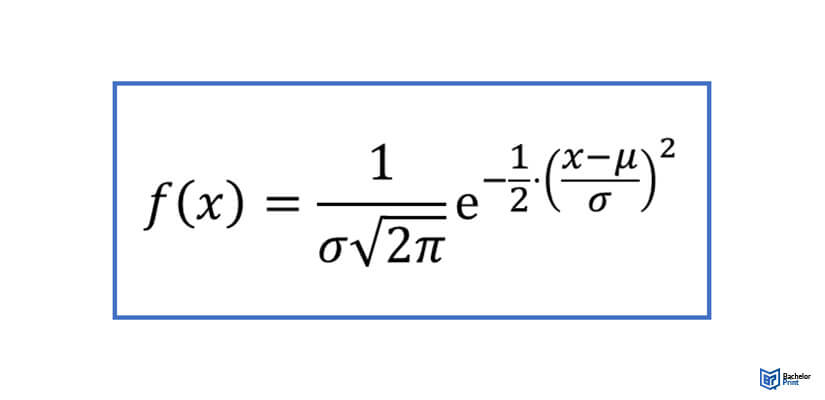
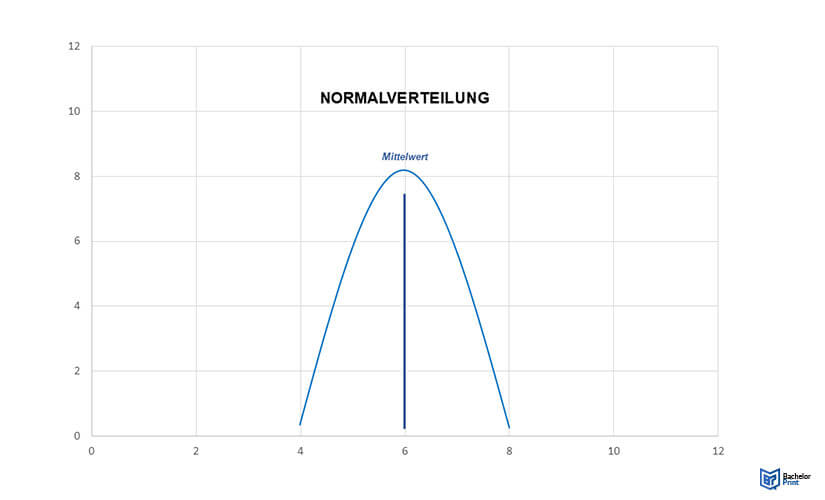
Normalverteilung mithilfe des Graphs verstehen
Die sogenannte Glockenkurve entsteht, wenn du die Häufigkeit (Anzahl der Gebäude bzw. der erhobenen Personen) an der y-Achse einträgst und die jeweiligen Daten (Schulabschluss, Altersgruppe oder Höhe der Gebäude) an der x-Achse. So ist der Zenit der Kurve stets in der Mitte, sodass du dort den Mittelwert auch ohne Berechnung ablesen kannst.
Allgemein ausgedrückt bildet der Graph der Normalverteilung die Verteilung der Daten um den Mittelwert ab. Bei einer symmetrischen Kurvendarstellung der Körpergröße der Bevölkerung zeigt der Mittelwert die höchste Körpergröße (y-Achse) mit der entsprechenden Altersgruppe (x-Achse).
Rechts und links davon werden all diejenigen dargestellt, die kleiner sind. Da dies sowohl in höherem als auch in jüngerem Alter und sowohl bei männlichen als auch bei weiblichen Menschen vorkommt, ist die Kurve bei dieser Erhebung in der Regel symmetrisch.
Veränderungen im Graphenverlauf erkennen und benennen
Die Stelle des Mittelwerts wird auf der x-Achse mit µ=0, dem sogenannten «Erfahrungswert» gekennzeichnet. Abweichungen von dieser Mittellinie werden links der Mittellinie mit µ minus Sigma (klein geschrieben), µ minus 2 Sigma (klein geschrieben) und so fortlaufend beschriftet.
Rechts der Mittellinie wird entsprechend µ plus Sigma (klein geschrieben) und fortlaufend beschriftet. Das klein geschriebene Sigma steht für die Standardabweichung und gibt die absolute Streuung an.
Häufig gestellte Fragen
Um große Datenmengen und darin Häufigkeiten der Daten und Beobachtungen mithilfe des Graphen anschaulich darstellen zu können. Die Werte lassen sich dort schnell und einfach ablesen, sodass eine grobe Interpretation sofort möglich ist.
Die Formel folgt dem mathematischen Weg zum Ergebnis und liefert insbesondere bei Abweichungen handfeste Ergebnisse.
Nein – bei Abweichungen der Werte kann sich der Graph nach links oder rechts verschieben. Dabei kann sich auch die Form der Kurve deutlich von gestreckt bis gestaucht verändern. Genau genommen entsteht also nicht immer eine Darstellung in «Glockenform».
Die Wahrscheinlichkeit kommt in der Statistik dann ins Spiel, wenn wir Dinge berechnen wollen, deren Daten einen hohen Anteil von Zufall haben. So beispielsweise die Berechnung, wie viele Schüsse auf eine Torwand wirklich treffen und wie viele beziehungsweise welche Abweichungen es gibt.3
Die Stauchung entsteht, wenn der Wert von µ sich von 0 auf 2 erhöht und gleichzeitig Sigma (klein geschrieben) von 1 auf Sigma (klein geschrieben) = 2 ansteigt. Anders ausgedrückt ist der Mittelwert höher als bei der Normalkurve, die Streuung aber ebenfalls. Dadurch wird die Kurve flacher oder «gestaucht».
Quellen
1 Statista GmbH: Definition Normalverteilung, in: Lexikon, o.D. [online] https://de.statista.com/statistik/lexikon/definition/95/normalverteilung/ (abgerufen am 23.01.2023)
2 Universität Oldenburg: Beispiele und Aufgaben im Modul Normalverteilung, in: ViLeS, 2019 [online] https://viles.uni-oldenburg.de/navtest/viles2/kapitel02_Theoretische~~lVerteilungen/modul02_Normalverteilung/ebene02_Beispiele~~lund~~lAufgaben/02__02__02__01.php3 (abgerufen am 23.01.2023)
3 Novustat GmbH: Warum Sie Experte für die Normalverteilung werden sollten – erklärt mit Beispielen, in: novustat.com, 2019 [online] https://novustat.com/statistik-blog/normalverteilung-erklaert-mit-beispielen.html (abgerufen am 23.01.2023)
