
Der Hypothesentest ist ein Kernelement wissenschaftlicher Arbeit. Er prüft datenbezogene Aussagen auf ihre (wahrscheinliche) Korrektheit, indem er die Gegenthese zur Debatte stellt. In diesem Beitrag erhältst du einen Überblick über die wichtigsten Informationen zum Hypothesentest.
Definition: Hypothesentest
Der Hypothesentest ist eine Methode, um wissenschaftliche Aussagen zu überprüfen. Ihr Hauptmerkmal besteht in der Gegenüberstellung von Nullhypothese und Alternativhypothese. Im Rahmen des Hypothesentests wird die Nullhypothese vorläufig angenommen. Sie gibt im Wesentlichen vor, dass keine auffällige Datenlage, Korrelation (o.Ä.) festzustellen ist. In den meisten wissenschaftlichen Arbeiten handelt es sich bei der Nullhypothese also um die Gegenthese zum beabsichtigten Erkenntnisgewinn. Die Alternativhypothese beinhaltet dagegen die (vermeintliche) Neuheit, die es (wenn möglich) zu beweisen gilt. Wird die Nullhypothese für falsch befunden, ist dies ein Beitrag zum Beweis der Arbeitshypothese. Generell gilt jedoch: Der Hypothesentest erlaubt nur Aussagen darüber, dass eine These wahrscheinlich wahr oder falsch ist. Einen zweifelsfreien Beweis liefert sie nicht.
Durchführung eines Hypothesentests
Um einen Hypothesentest durchzuführen, musst du die zu überprüfende These in ein Hypothesenpaar aus Nullhypothese H0 und Alternativhypothese H1 übersetzen. Anschließend wählst du anhand des behandelten Datentypus und der Bedürfnisse deiner Fragestellung eine geeignete Variante des Hypothesentests. Es gibt eine große Auswahl unterschiedlicher Testarten, die dich zu verschiedenen Aussagen befähigen. Ferner benötigst du einen Wert für das Signifikanzniveau, durch das ermittelt wird, ab wann die Werte einen kritischen Bereich k betreten, der die These falsifiziert. Anschließend ermittelst du die nötigen Daten in Form einer Stichprobe. Schließlich führst du die gewählte Testvariante anhand der ermittelten Werte aus.
1. Aufstellen von Hypothesen
Jeder Hypothesentest benötigt eine Null- und eine Alternativhypothese. Die Nullhypothese wird mit der Variable H0 angegeben, die Alternativhypothese mit der Variable H1. Die Nullhypothese sagt aus, dass aus den Daten nichts hervorgeht, das eine (neu) vermutete Annahme verifizieren könnte. Die Alternativhypothese wiederum sagt aus, dass durchaus Daten vorliegen, um eine neue Annahme zu verifizieren.¹ Angenommen, man wolle die (steile) Arbeitsthese prüfen, höchstens 30 Prozent der Bevölkerung wären leidenschaftliche Ravioli-Esser, dann bestünde der Hypothesentest aus:
H0 = Mehr als 30 Prozent der Bevölkerung sind leidenschaftliche Ravioli-Esser. (H0 : p0 > 0,3)
H1 = Weniger als 30 Prozent der Bevölkerung sind leidenschaftliche Ravioli-Esser. (H1 : p1 < 0,3)
2. Datenerhebung
Üblicherweise wird der Hypothesentest bei Stichproben angewandt, um diese in ein Verhältnis zur Grundgesamtheit zu setzen. Die Entnahme der Stichprobe sollte den erforderlichen Standards deines Fachbereichs entsprechen und eine aussagekräftige Zahl möglichst zufällig betrachteter Elemente/Probanden umfassen.
3. Statistischer Test
Die wichtigsten Arten des Hypothesentests sind der links- und rechtsseitige Signifikanztest, der beidseitige Signifikanztest und der Alternativtest.
Darüber hinaus gibt es Testarten, die mehrere Gruppen von Variablen betrachten. Der Wilcoxon-Mann-Whitney-Test vergleicht etwa die Werte zweier unabhängig entstandener Stichproben. Der Wilcoxon-Vorzeichen-Rang-Test vergleicht voneinander abhängige Stichproben im Hinblick auf einen bestimmten Wert, während der Friedmann-Test Daten aus mindestens drei Gruppen (abhängiger Stichproben) vergleicht.
Die Wahl des richtigen Testverfahrens hängt von der Menge der Stichproben sowie vom Wertebereich ab, der zu ihrer Verifizierung relevant ist. Für das Ravioli-Beispiel verwenden wir einen linksseitigen Signifikanztest.
4. Annahme oder Ablehnung der Null-Hypothese
Nachdem wir die Daten erhoben und uns für einen Test entschieden haben, können wir die Nullhypothese verifizieren oder falsifizieren. Dazu musst du zunächst das Signifikanzniveau feststellen. Dies ist die Irrtumswahrscheinlichkeit deiner Stichprobe. Im Hinblick auf das Beispiel der Ravioli-Esser wollen wir davon ausgehen, dass das Signifikanzniveau 5 Prozent und die Zahl der Befragten 100 beträgt. Das heißt, dass die Antworten von 100 Befragten mit einer Wahrscheinlichkeit von 5 Prozent statistisch nicht der Verteilung in der Grundgesamtheit entsprechen. Anschließend gilt es, in der sogenannten Fisher-Tabelle die kumulierte Wahrscheinlichkeit respektive den kritischen Wert auszulesen, der die statistische Schwankung bei (in diesem Fall) 100 Befragten mit einer Irrtumswahrscheinlichkeit von 5 Prozent und dem Annahmewert p = 0,3 (für die 30 Prozent Ravioli-Esser) angibt. Dafür suchen wir nach der Wahrscheinlichkeit k, bei der p gerade kleiner oder gleich der Irrtumswahrscheinlichkeit von 5 Prozent ist. Für den Ravioli-Fall gilt k = 22. Das bedeutet schlussendlich, dass wenn 23 oder mehr Befragte angeben, sie wären leidenschaftliche Ravioli-Esser, die Nullhypothese anzunehmen ist. Liegt der Wert bei 22 oder weniger, wurde die Nullhypothese falsifiziert.
Einseitige und beidseitige Hypothesentests
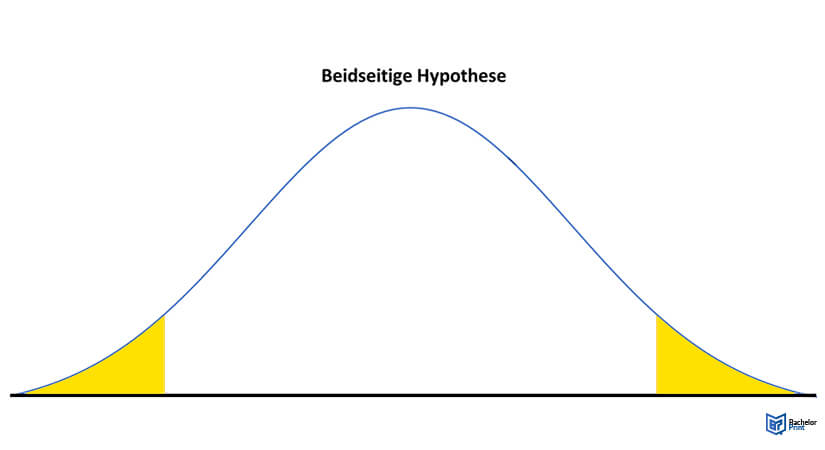
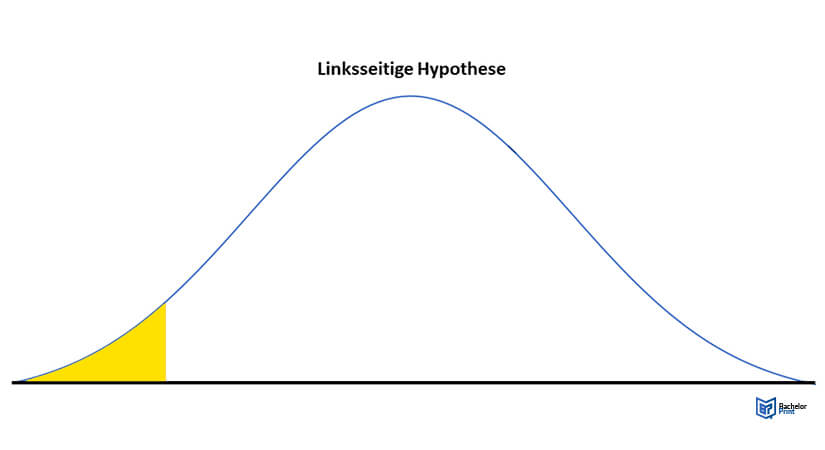
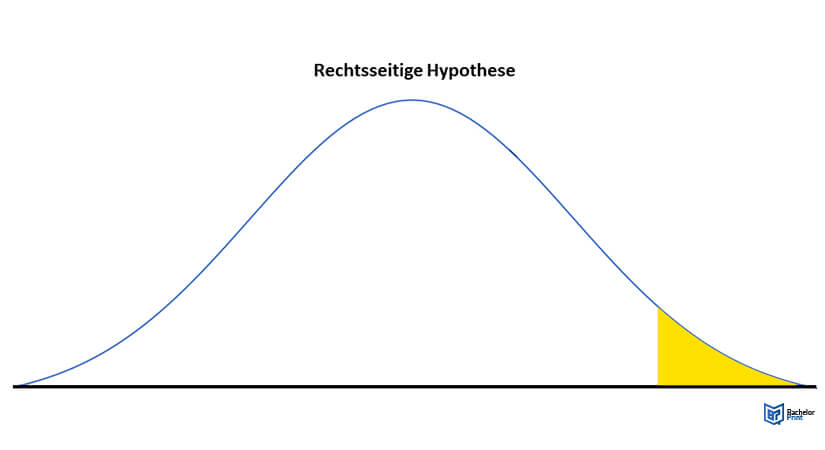
Es gibt zwei einseitige Hypothesentests. Diese sind der linksseitige und der rechtsseitige Signifikanztest. Der linksseitige Signifikanztest zielt darauf ab, der Hypothese nachzugehen, dass der zu ermittelnde Wert größer ist als bislang angenommen. Der rechtsseitige Signifikanztest orientiert sich an der Hypothese, dass der gesuchte Wert kleiner ist. Der beidseitige Signifikanztest geht davon aus, dass der gesuchte Wert (egal in welche Richtung) anders ist.²
Beidseitiger Hypothesentest
Linksseitiger Hypothesentest
Rechtsseitiger Hypothesentest
Hypothesentest – Mögliche Fehler
Der Hypothesentest birgt zwei inhärente Fehlermöglichkeiten. Beim Fehler 1. Art wird die Nullhypothese verworfen, obwohl sie wahr ist. Beim Fehler 2. Art wird die Nullhypothese bestätigt, obwohl sie falsch ist.³
| Fehler 1. Art | Fehler 2. Art |
| Ein Fehler 1. Art liegt vor, wenn der Hypothesentest ergibt, dass Menschen keine Ravioli mögen, weil sie diese ablehnten, als man sie ihnen anbot. In Wirklichkeit mögen sie Ravioli aber sehr gerne und hatten während der Datenerhebung lediglich keinen Hunger. Der Fehler 1. Art verweist auf die Irrtumswahrscheinlichkeit im Signifikanzniveau. Als gängiger Richtwert gilt ein Signifikanzniveau von 5 Prozent. |
Ein Fehler 2. Art liegt vor, wenn der Hypothesentest ergibt, dass Menschen Ravioli mögen, weil sie während der Datenerhebung viel davon aßen. In Wirklichkeit wurde die Datenerhebung jedoch in einem Studentenwohnheim durchgeführt, das überdurchschnittlich viele Ravioli-Enthusiasten beherbergt und nicht die Gesamtbevölkerung repräsentiert. Liegt ein Fehler 2. Art vor, muss die Form der Datenerhebung (und gegebenenfalls das Signifikanzniveau) angepasst werden. |
Häufig gestellte Fragen
Der Hypothesentest ist eine wissenschaftliche Methode, welche die (wahrscheinliche) Validität einer Aussage anhand ihrer Gegenaussage überprüft. Der Hypothesentest kommt vornehmlich bei der Analyse von Stichproben zum Einsatz.
Wenn die Datenlage keine sichere Aussage darüber zulässt, ob eine These als wahr oder falsch zu bewerten ist, kann der Hypothesentest zur Argumentation beitragen. Hypothesentests ermöglichen nicht, die Ausgangsthese vollständig zu verwerfen, erlauben jedoch Aussagen zur Irrtumswahrscheinlichkeit.
Da Hypothesentests oft zur Überprüfung von Stichproben angewandt werden, eignen sie sich auch für Arbeiten mit kleinerem Umfang wie Seminar- und Bachelorarbeiten.
Ein Hypothesentest kann Aussagen verwerfen, die eigentlich wahr sind (Fehler 1. Art) oder Aussagen bestätigen, die eigentlich falsch sind (Fehler 2. Art).
Der Hypothesentest kann durchgeführt werden, sobald eine Nullhypothese und eine Alternativhypothese feststehen. Ferner sind Stichproben(-daten) für einen Hypothesentest erforderlich.
Quellen
¹ Edenfeld, Fabian: Vergleich und Implementierung
von Hypothesentests für das
statistische Model Checking, in: Westfälische Wilhelms-Universität Münster, 04.2017, [online] https://www.uni-muenster.de/imperia/md/content/informatik/agremke/edenfeld_vergleich_und_implementierung__von_hypothesentest_fu__r_das_statistische_model_checking.pdf (19.08.2022)
² Prof. Dr. Schumacher, Markus; Dr. Lai, Stan: Statistische Methoden der Datenanalyse, in: Albert-Ludwigs-Universität Freiburg, o.D., [online] https://terascale.physik.uni-freiburg.de/lehre/ws_1213/Vorlesungsfolien/StatistischeHypothesen2 (19.08.2022)
³ Otto-von-Guericke-Universität Magdeburg: Induktive Statistik: Otto-von-Guericke-Universität Magdeburg, o.D., [online] http://fma2.math.uni-magdeburg.de/~mathww/POTT/mathIII/76_88.pdf (19.08.2022)